Unified model scales pressure fluctuation in an accelerated liquid

A research team from Japan has developed a unified model to scale the transitional pressure development in a one-dimensional flow. This achievement provides a better understanding of how pressure fields build up in the confined fluid system for various acceleration situations, which might be applicable to biomechanics-related impact problems, such as human brain injuries caused by physical contact.

Liquid is usually not considered compressible, except for when subjected to a high-speed flow or rapid acceleration. The latter case is known as the water hammer theory, which often occurs with a loud sound when a water faucet is suddenly closed.

In recent years, the onset of mild traumatic brain injury has been discussed in a similar context, meaning that better understanding of this issue is important in not only traditional engineering but also emerging biomechanics applications.

An open question in this classic problem is how to model the transitional development of the pressure field during acceleration.

Existing works often rely on either the incompressible or compressible assumptions (i.e., the water hammer theory), in which the acceleration duration is considered so short that the pressure wavefront develops as a step-wise function (i.e., the pressure in the liquid jumps from zero to a fully developed state spontaneously).

However, in biomechanical impact, the impactors are typically soft, and the impact duration should be significantly longer.

At the Tokyo University of Agriculture and Technology (TUAT), a research team from the Department of Mechanical Systems Engineering has developed a scaling model of transitional pressure development while employing a newly modified dimensionless number.

The study is published in the Journal of Fluid Mechanics.

The research team, led by Prof. Yoshiyuki Tagawa, including Chihiro Kurihara (a master’s graduate) and Akihito Kiyama (former assistant professor at TUAT, now at Saitama University).

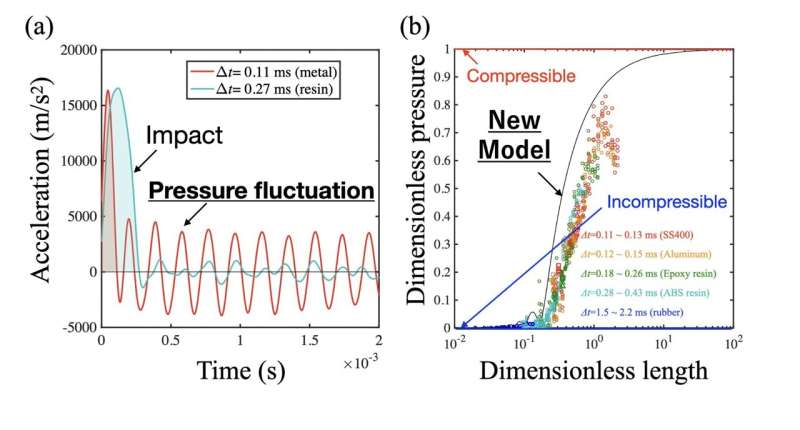
The team came up with a simple experimental setup in which a test tube partially filled with a liquid was dropped freely and eventually collided with floors of various stiffness. The acceleration conditions, which are primary parameters for this specific case, can be tuned with the liquid column length, the speed of sound of liquid (i.e., liquid type), and the acceleration duration (i.e., the floor stiffness).

These parameters determine a dimensionless number, Strouhal number St, which is redefined as the ratio of the fluid length to the thickness of the pressure wavefront. While this dimensionless number is often understood as the ratio of fluid/acoustic timescales, the interpretation is more intuitive in this system.

With the help of indirect pressure measurements inside the liquid using an accelerometer, the team proposed an analytical model that interconnects the dimensionless pressure and the Strouhal number.

Their systematic experiment showed that the proposed model can be applied universally to various floors and liquid types. The model was robust even for a weak hydrogel. Even though the model is designed for a one-dimensional system such as a pipe, the concept could be developed into a three-dimensional system in the future.

“Our finding is significantly important for understanding pressure dynamics in confined fluid systems under various acceleration conditions,” said Tagawa.

“Our research has revealed a unified scaling model that bridges incompressible and compressible flow theories, which can be used to improve engineering designs and to study impact-related biomechanics, such as mitigating brain injuries caused by physical impacts.”