Scientists map the mathematics behind how we create and innovate

A new study in Nature Communications explores the dynamics of higher-order novelties, identifying fascinating patterns in how we combine existing elements to create novelty, potentially reshaping our understanding of human creativity and innovation.

Novelties—a common part of human life—refer to one of two things. The first is the discovery of a single item, like a place, song, or an artist. The second covers discoveries new to everyone, such as technological developments or drug discoveries.

The researchers in this study aimed to understand how both kinds of novelties emerge. The team was led by Prof. Vito Latora from the Queen Mary University of London, who spoke to Phys.org about the work.

“I have always been attracted by creativity and innovation, which are the driving forces of human progress. This paper is one of a sequence of theoretical and applied works of my research group to study and model the mechanisms underlying creativity, with the goal of understanding what makes a new idea, team, product, or technology successful,” said Prof. Latora.

The team analyzed real-world data from three sources to study higher-order novelties.

First-time appearances

One of the main challenges with studying novelties is that most previous research has focused on first-order novelties, i.e., first-time appearances of individual elements.

For example, eating something new or visiting a new place for the first time. However, this approach overlooks an important innovation mechanism—combining existing elements to create something new.

For example, words can be strung together in different ways to create new poetry or stories, or musical notes can be combined to create a whole new song. The latter is known as higher-order novelties.

Prof. Latora said, “In our study, we introduced and explored a more general notion of novelty, which we named higher-order novelty, defined as the first time two or more elements appear together in a sequence.”

To simulate how these combinations occur, the research team developed a framework called Edge-Reinforced Random Walk with Triggering or ERRWT.

Random walk and ERRWT

The ERRWT model is based on the random walk, a mathematical model that describes the evolution of a system based on discretized steps. In this method, the next position of the walker depends only on its current position.

The movement between positions is completely random, with each movement in each direction having equal probabilities.

Prof. Latora explained the process: “Imagine all the items we can explore, or all the ideas that we can have can be described as the nodes of a network, whose links represent relations or similarity between two items or concepts.”

The model’s innovation lies in how it simulates the evolution of these networks. As the walker moves through the network, it doesn’t just traverse existing paths—it creates new connections, triggering the emergence of new nodes, mirroring how real-world discovery processes expand our horizon of possibilities.

The creation of new connections—when novel combinations occur—is known as edge triggering, and the strengthening of connections between frequently used combinations is known as edge reinforcement.

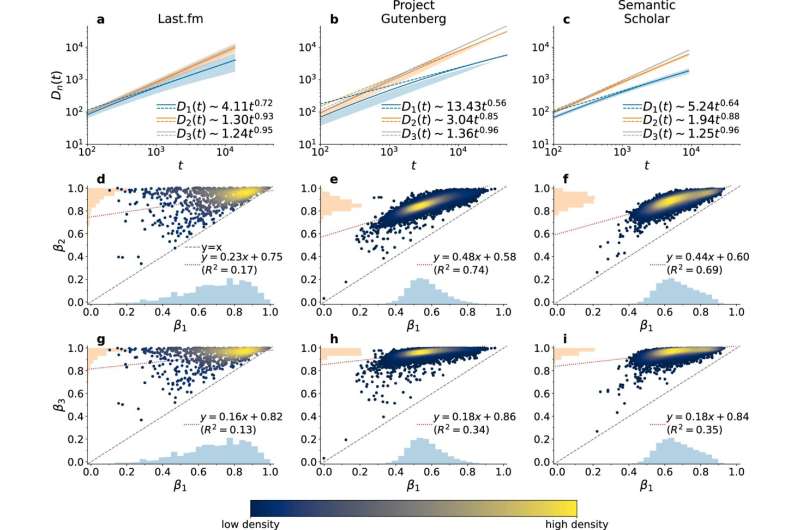
The team used this ERRWT model to analyze three datasets. They chose to analyze music listening patterns (Last.fm), literary texts and books (Project Gutenberg), and scientific articles (Semantic Scholar).

Prof. Latora explained how the model works, saying, “The more we listen to a song or we associate two songs, the higher is the probability that we will repeat the song or the association in the future. Moreover, this also implies that the discoveries of new songs or associations generate an expanding space of opportunities that are only available to us in the moment we unlock what is adjacent to them.”

Heaps’ law

The team discovered that the combinations followed predictable patterns, governed by Heaps’ law, a power-law growth relationship. This is a mathematical relationship that describes how new combinations emerge over time, offering a quantitative way to measure and predict innovative processes.

According to their simulations, different processes can have the same rate of discovering individual elements but very different rates of discovering combinations.

More specifically, they found that for the Last.fm dataset, users with the same rate of discovering new songs can have very different paths in how they sequence these songs.

For the literature dataset, they found that writers tend to generate new word associations more often than introducing new words. Finally, scientific articles showed more creative word combinations compared to narrative texts, especially in paper titles.

The ERRWT showed how network structure and exploration patterns co-evolve, demonstrating that reinforcement (strengthening existing paths) and triggering (creating new connections) are necessary to explain real-world patterns.

Implications and future work

The new framework provides a new basis for understanding innovation and creativity, bridging the gap between individual discovery and combinatorial innovation.

The findings help us understand the relevance of this model, especially seeing how new scientific discoveries emerge from combinations of existing knowledge. It could also inform educational approaches to creativity.

Prof. Latora commented, “Studying creative processes and understanding how new ideas emerge and how novelties can trigger further discoveries is fundamental, if we want to devise effective interventions to nurture the success and sustainable growth of our society. We believe that our findings and proposed models can be directly used to answer questions about the rise and fall of popular items or ideas.”

The research team aims to generalize the model further and also include a social component, which is presently missing.

© 2025 Science X Network